En neuropsychologie et en logopédie on utilise de très nombreux tests standardisés. Un test standardisé a été étalonné sur une population tout-venant, ce qui signifie que pour chaque tranche d’âge ou chaque tranche de degré scolaire, les normes du test nous indiquent quelles sont les performances moyennes attendues, mais surtout également quel écart est observé autour de la moyenne. Cela permet de situer une performance obtenue et de dire si l’écart par rapport à la moyenne est normal (donc fréquemment observé) ou atypique (très rare). Chaque individu est comparé à un échantillon équivalent en âge et/ou niveau scolaire et/ou niveau de formation.
La plupart des phénomènes naturels (le poids et la taille par exemple) suivent une distribution dite « normale » ou « de Gauss », une courbe en cloche où l’on constate que la majorité des individus se situent vers la moyenne et que plus on s’écarte de la moyenne, plus le phénomène devient rare (par ex. il y a très peu de très petites personnes et très peu de géants).
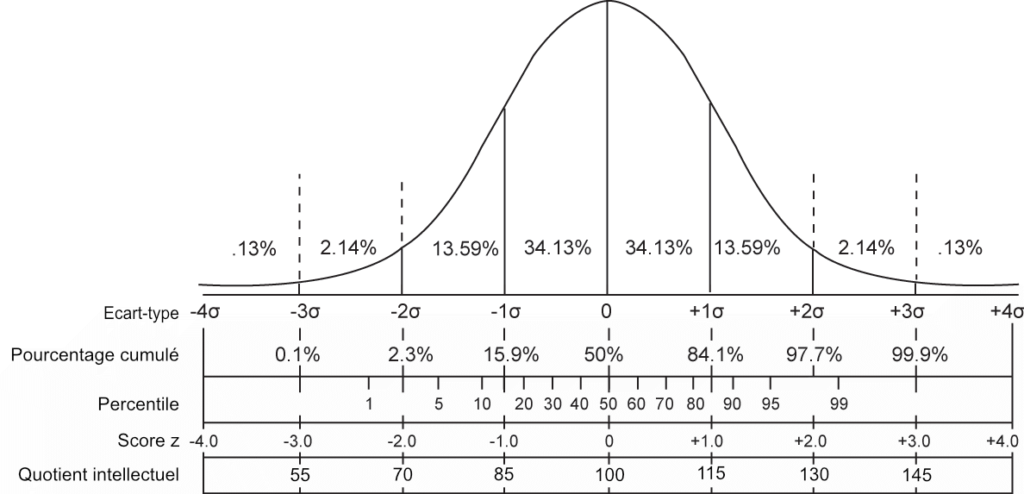
La figure ci-dessous illustre cette distribution, la courbe de Gauss :
Quel que soit le test utilisé, on transforme les résultats en scores normés de diverses sortes:
- percentiles : la moyenne (percentile 50) est le point où 50% des individus se situent en dessous et 50% en dessus. Ainsi, le percentile 2 signifie qu’on se situe dans les 2% inférieurs (ou que 98% des individus se situent au dessus de cette valeur).
- scores z : mesure de l’écart-type (sigma) par rapport à la moyenne. La moyenne correspond donc au score z = 0. Pour z = -1 on se situe au percentile 16 et pour z = -2 on se situe dans les 2% les plus faibles. Attention, la relation « score z – percentile » n’est pas linéaire mais elle est régie par une formule très complexe. Par exemple avec un score z = -1.3 on est déjà au percentile 10.
- les notes standard (n.s.) ont une moyenne de 10 et un écart-type de 3. Ainsi, une note standard de 4 correspond à -2 écart-types et donc au 2% inférieurs, alors qu’une note standard de 15 correspond au 5% supérieurs.
- le quotient intellectuel (QI) suit une distribution dont la moyenne est de 100 et l’écart-type de 15. Lorsqu’on possède un QI de 130 on se situe dans les 2% supérieurs.